We live in a time when privacy matters more than ever. From online banking to healthcare records, our data constantly flows through digital systems. The risk of data breaches has never been higher, making data protection one of the most talked-about concerns in modern technology. This is where Homomorphic Encryption shines. It allows organizations to process encrypted data without ever needing to reveal the original content.
Homomorphic Encryption stands out because it protects sensitive information even during computation. Companies, researchers, and developers see this as a game-changer. It combines privacy, security, and efficiency in a way that traditional encryption cannot match. This technology is essential in advanced technology fields like cloud computing, artificial intelligence, and big data analytics.
Let’s explore what Homomorphic Encryption is, why it matters, and how it’s already reshaping the digital world.
What is Homomorphic Encryption
It is a form of encryption that enables calculations on encrypted data. These calculations produce results that, once decrypted, match the outcome of operations performed on the original data.
To put it simply, this encryption method lets you work with data while keeping it hidden. This makes it perfect for secure data processing, especially when sensitive information must be shared with third parties.
Some related terms include:
- Fully Homomorphic Encryption (FHE)
- Partial Homomorphic Encryption (PHE)
- Somewhat Homomorphic Encryption (SHE)
All these variations fall under the same family but differ in what kinds of calculations they allow.
Breaking Down Homomorphic Encryption
Let’s take a closer look at how this technology works. When you encrypt something, you usually scramble the data into unreadable text. Traditional encryption requires you to decrypt that data to perform any useful operations. This can be dangerous because the data becomes vulnerable during that brief moment when it’s readable.
This approach changes that completely. It allows a system to carry out tasks on encrypted information without ever revealing the actual data. Think of it as locking your groceries in a box, then asking someone to prepare a meal without unlocking it. At the end, you open the box and see the finished dish.
There are a few key parts that make this possible:
The Encryption and Decryption Keys
Encryption turns plain data into ciphertext using a public key. Decryption brings it back to its original form using a private key. In Homomorphic Encryption, this process becomes more complex due to the extra mathematical operations it must support.
Supported Operations
Depending on the type, this encryption supports one or more arithmetic operations like addition and multiplication. Fully Homomorphic Encryption supports both, which makes it highly versatile.
Imagine a hospital collecting health data. Instead of decrypting this data to analyze it for trends or risks, the hospital can send the encrypted data to a cloud server. The server runs the analysis while the data stays encrypted. When the results return, the hospital decrypts them to see the insights, without ever compromising patient privacy.
Security
This relies on hard mathematical problems, often from lattice-based cryptography, to protect data. Even with modern computing power, this type of encryption remains extremely difficult to crack.
This level of security is essential in industries where trust and confidentiality are non-negotiable.
History
The journey of this encryption scheme began as a theoretical concept but has since evolved into a working technology.
| Year | Development |
|---|---|
| 1978 | Researchers Rivest, Adleman, and Dertouzos propose the idea of privacy-preserving computation. |
| 2009 | Craig Gentry develops the first practical Fully Homomorphic Encryption (FHE) scheme. |
| 2010s | Continued improvements in performance and reduced computational cost. |
| Present | Tech giants and startups explore real-world applications in healthcare, cloud computing, and finance. |
Before 2009, many believed that Homomorphic Encryption would remain a mathematical dream. Gentry’s work proved otherwise and sparked rapid growth in the field.
Types of Homomorphic Encryption
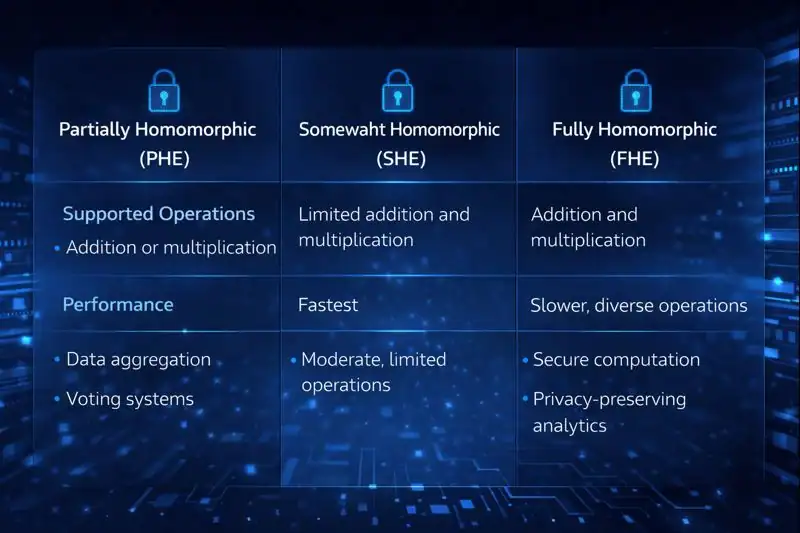
Homomorphic Encryption comes in three main types. Each supports different kinds of operations and use cases.
Partially Homomorphic Encryption (PHE)
Supports only one operation: either addition or multiplication. This is simpler and faster but limited in functionality.
Somewhat Homomorphic Encryption (SHE)
Allows both addition and multiplication but only a limited number of times. It’s a middle ground between speed and flexibility.
Fully Homomorphic Encryption (FHE)
Supports unlimited additions and multiplications. This is the most powerful type but also the most demanding in terms of computing resources.
| Type | Operations Supported | Performance | Use Case |
|---|---|---|---|
| PHE | Addition or Multiplication | Fast | Simple tasks |
| SHE | Limited Addition and Multiplication | Moderate | Controlled environments |
| FHE | Full Algebraic Operations | Slower | Complex cloud-based analytics |
How does Homomorphic Encryption work?
At a high level, the system encrypts the input, performs mathematical operations on the encrypted data, and then decrypts the final result. These steps happen without ever exposing the original data to any party during processing.
This process uses special algebraic techniques and complex number theory. While these methods are computationally intensive, they allow full privacy during processing, which is a huge advantage in sensitive environments.
For example, a voting system can tally encrypted votes, and only after the computation does it decrypt the final count. This keeps individual votes private throughout the process.
Pros & Cons
This encryption model sounds like a dream, but it also comes with trade-offs.
| Pros | Cons |
|---|---|
| Keeps data encrypted during use | Requires more computational power |
| Enables secure collaboration | Slower than traditional encryption |
| Meets regulatory requirements | Fewer available tools |
| Reduces data breach risks | More complex to implement |
Despite the cons, researchers continue to make improvements. What once took hours now takes minutes, and soon it could take seconds.
Uses of Homomorphic Encryption
Homomorphic Encryption finds use in industries where privacy, security, and compliance matter most.
Healthcare
Hospitals and researchers can run machine learning models on encrypted patient data to discover health trends. This helps them maintain compliance with laws like HIPAA and GDPR while still advancing medical science.
Financial Services
Banks and fintech platforms can calculate credit scores or detect fraud on encrypted data. This protects users from internal and external threats while maintaining service quality.
Cloud Computing
Cloud service providers can analyze encrypted workloads without ever seeing the data. This makes it possible for companies to use external services without compromising their confidential files.
Government & Public Sector
Governments can use Homomorphic Encryption for secure voting systems, confidential communication, and census data analysis. These operations benefit from high-level privacy and reduced risks of leaks or interference.
Resources
- TechTarget. Homomorphic Encryption: Secure Data Processing in the Cloud
- PhoenixNAP. Homomorphic Encryption Explained
- FreeCodeCamp. Homomorphic Encryption in Plain English
- GeeksForGeeks. Homomorphic Encryption Overview
- IBM. How IBM is Advancing Homomorphic Encryption
